Entendendo a Teoria por Trás do PCA (Análise de Componentes Principais)

A Análise de Componentes Principais (PCA – Principal Component Analysis) é uma técnica estatística utilizada para transformar um conjunto de variáveis possivelmente correlacionadas em um conjunto de variáveis linearmente independentes chamadas de componentes principais. O PCA é amplamente utilizado em aprendizado de máquina para redução de dimensionalidade, compressão de dados e visualização.

Aqui estão 10 exemplos detalhados de aplicação da Análise de Componentes Principais (PCA) em diferentes áreas:

1. Compressão de Imagens

PCA é amplamente utilizado na compressão de imagens para reduzir a quantidade de dados sem sacrificar a qualidade visual. Por exemplo, uma imagem de alta resolução pode ter milhares de pixels. Com o PCA, é possível identificar os principais componentes que capturam a maior parte das variações da imagem. Ao projetar a imagem nesses componentes, o tamanho do arquivo pode ser reduzido significativamente, mantendo ainda uma boa representação da imagem original.

Exemplo: Um arquivo de imagem com 1 milhão de pixels pode ser reduzido para um arquivo de 10 mil componentes principais, diminuindo o tamanho do arquivo sem grande perda de qualidade.

2. Análise de Expressão Gênica em Biologia

Em estudos genéticos, os cientistas trabalham com dados de expressão gênica de milhares de genes simultaneamente. PCA é utilizado para reduzir a dimensionalidade desses dados complexos, destacando os genes mais relevantes. Isso permite identificar padrões nos genes que possam estar associados a certas doenças, como câncer.

Exemplo: Em uma pesquisa de câncer, PCA pode ser usado para analisar 20 mil genes e reduzir isso a 100 componentes principais que explicam a maior parte da variação nos dados de expressão gênica, facilitando a identificação de padrões.

3. Reconhecimento Facial

No reconhecimento facial, o PCA é utilizado para extrair as principais características dos rostos de várias pessoas, como a forma e a posição dos olhos, nariz e boca. Essas características são usadas para representar os rostos de forma simplificada. O PCA ajuda a diminuir a quantidade de dados necessários para processar e reconhecer um rosto em um banco de dados.

Exemplo: Ao capturar 100 mil pixels de uma imagem facial, o PCA pode reduzir essa quantidade para apenas 300 componentes principais, que ainda representam o rosto com precisão.

4. Análise de Mercado no Setor Financeiro

PCA é utilizado por analistas financeiros para reduzir a complexidade dos dados do mercado, como preços de ações, indicadores econômicos e taxas de câmbio. Ele ajuda a identificar as principais variáveis que afetam o desempenho do mercado e remove a redundância nos dados.

Exemplo: Um analista pode usar PCA para reduzir um conjunto de 200 variáveis do mercado (como o preço de ações de diferentes setores) para 5 componentes principais que capturam as principais tendências e comportamentos do mercado.

5. Previsão do Clima

Dados climáticos incluem múltiplas variáveis como temperatura, pressão, umidade e vento. PCA é utilizado para simplificar esses dados em componentes principais que refletem as principais variações climáticas. Isso permite prever padrões de clima, como o El Niño.

Exemplo: Em vez de analisar milhares de medições diárias de temperatura e pressão, os meteorologistas podem reduzir esses dados para poucos componentes principais que capturam a variabilidade climática global.

6. Análise de Dados Demográficos

Em estudos demográficos, PCA é usado para identificar as características mais significativas de grandes populações. Ao trabalhar com variáveis como renda, nível de escolaridade, ocupação e moradia, o PCA ajuda a identificar padrões demográficos, como grupos de alta renda ou áreas com baixo nível de escolaridade.

Exemplo: Uma pesquisa demográfica com 50 variáveis (renda, educação, ocupação) pode ser reduzida para 3 componentes principais que capturam as variações mais importantes entre diferentes populações.

7. Processamento de Sinais de Eletroencefalograma (EEG)

No estudo de atividades cerebrais, os pesquisadores utilizam EEGs para capturar sinais do cérebro em várias frequências. Como o número de sinais capturados pode ser alto, o PCA é aplicado para reduzir os dados e focar nos principais padrões de ondas cerebrais, como alfa, beta e delta.

Exemplo: Um EEG captura dados de 128 sensores. Com o PCA, os pesquisadores podem reduzir esses dados para 10 componentes principais que explicam a maior parte da atividade cerebral, facilitando o diagnóstico de distúrbios neurológicos.

8. Análise de Preferências de Consumidores

Empresas de marketing utilizam o PCA para entender as preferências dos consumidores em relação a produtos e serviços. Com questionários que capturam dezenas de características de produtos, como preço, qualidade e design, o PCA reduz as dimensões, identificando as principais preferências e agrupando consumidores com gostos semelhantes.

Exemplo: Um estudo com 50 variáveis de características de produtos pode ser reduzido para 3 componentes principais, representando a preferência por preço, qualidade e durabilidade, ajudando a segmentar o mercado.

9. Detecção de Fraudes Financeiras

PCA é aplicado na detecção de fraudes ao analisar grandes volumes de dados transacionais, como compras com cartão de crédito. Ele reduz as variáveis, destacando padrões anômalos que possam indicar atividades fraudulentas.

Exemplo: Dados de transações bancárias podem conter 100 variáveis (como valor da compra, localização, hora do dia). O PCA pode reduzir essas variáveis a 4 componentes principais que ajudam a identificar padrões suspeitos.

10. Visualização de Dados Multidimensionais

Muitas vezes, cientistas de dados usam PCA para visualizar dados multidimensionais em gráficos 2D ou 3D. Isso facilita a compreensão de padrões nos dados que seriam difíceis de interpretar em suas dimensões originais.

Exemplo: Um conjunto de dados com 10 variáveis (como características de clientes) pode ser reduzido para 2 componentes principais, permitindo que os dados sejam visualizados em um gráfico de dispersão 2D, facilitando a identificação de clusters.

Neste artigo, vamos nos aprofundar na matemática por trás do PCA, explorando seus fundamentos teóricos em detalhes.

O Problema: Dimensionalidade Alta

Imagine que você tenha um conjunto de dados com dezenas ou centenas de variáveis (ou features). Embora esses dados possam capturar muita informação, trabalhar com tantos atributos pode ser computacionalmente dispendioso. Além disso, muitos dos atributos podem ser redundantes ou fortemente correlacionados. Isso é conhecido como o problema da alta dimensionalidade.

O PCA aborda essa questão encontrando uma maneira de representar os dados em um espaço de menor dimensão, preservando o máximo de informação possível. A ideia é reduzir a dimensionalidade, sem perder a variância significativa dos dados.

Passo a Passo do PCA

O PCA pode ser dividido em algumas etapas principais. Vamos explorar cada uma delas em detalhes.

1. Normalização dos Dados

A primeira etapa essencial no PCA é a normalização dos dados. Isso é importante porque o PCA se baseia na variância, e a variância de uma variável depende da sua escala. Sem normalizar os dados, variáveis com escalas maiores dominariam o resultado do PCA.

Para normalizar, subtraímos a média de cada variável e dividimos pelo desvio padrão, tornando a média 0 e o desvio padrão 1.

Fórmula para normalizar uma variável ( x_i ):

[
x’_i = \frac{x_i – \mu}{\sigma}
]

Onde:

• ( x_i ) é o valor original da variável.
• ( \mu ) é a média da variável.
• ( \sigma ) é o desvio padrão da variável.

2. Construção da Matriz de Covariância

O PCA funciona através da análise da covariância entre as variáveis. A matriz de covariância é uma matriz quadrada que descreve como duas variáveis estão correlacionadas. A covariância mede o grau de variação conjunta entre duas variáveis.

Seja ( X ) um conjunto de dados com ( n ) variáveis e ( m ) amostras, a matriz de covariância ( C ) é dada por:

[
C = \frac{1}{m – 1} X^T X
]

3. Autovalores e Autovetores

Uma vez que temos a matriz de covariância, o próximo passo é calcular os autovalores e autovetores dessa matriz.

• Autovalores (( \lambda )) nos dizem a quantidade de variância explicada por cada componente.
• Autovetores são os componentes principais que representam as direções dos eixos no novo espaço de menor dimensionalidade.

Matematicamente, para a matriz de covariância ( C ), os autovalores e autovetores são encontrados resolvendo a seguinte equação:

[
C v = \lambda v
]

Onde ( v ) é o autovetor correspondente ao autovalor ( \lambda ). Cada autovetor representa uma nova direção no espaço de características.

4. Seleção dos Componentes Principais

Os componentes principais são os novos eixos que maximizam a variância dos dados projetados. Esses componentes principais são ordenados de acordo com os autovalores, de forma que o primeiro componente principal (( PC_1 )) captura a maior parte da variação dos dados, o segundo componente principal (( PC_2 )) captura a segunda maior parte, e assim por diante.

O número de componentes principais a serem mantidos depende de quanta variância você deseja preservar. Em muitos casos, uma fração significativa da variância dos dados pode ser capturada pelos primeiros poucos componentes.

A proporção de variância explicada é uma métrica importante no PCA. Ela é dada pela razão entre o autovalor de um componente principal e a soma de todos os autovalores:

[
\text{Proporção de Variância Explicada} = \frac{\lambda_i}{\sum_{i=1}^{n} \lambda_i}
]

5. Projeção dos Dados

O último passo do PCA é projetar os dados no novo subespaço definido pelos autovetores selecionados (componentes principais). Para isso, multiplicamos o conjunto de dados original pelos autovetores selecionados.

Se ( X ) for o conjunto de dados original e ( W ) a matriz dos autovetores (componentes principais), então os dados transformados ( Z ) são dados por:

[
Z = X W
]

O resultado ( Z ) é o conjunto de dados projetado em um espaço de dimensionalidade reduzida, preservando a maior parte da variância original.

Exemplo Numérico Simplificado

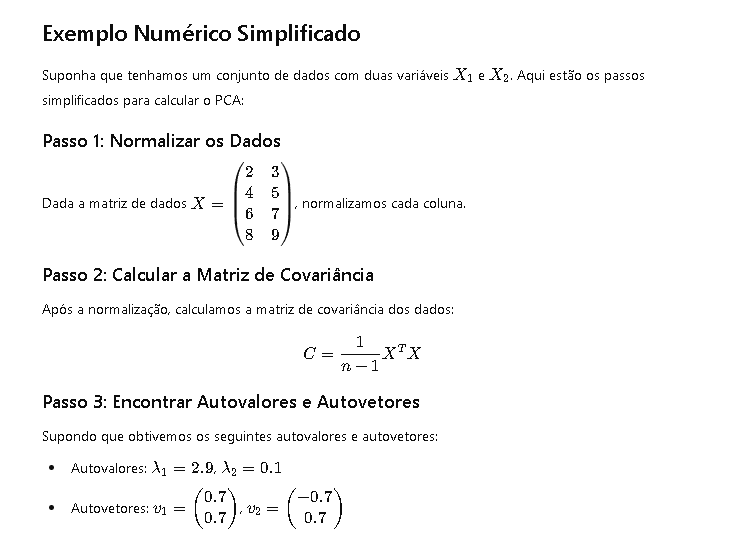
Suponha que tenhamos um conjunto de dados com duas variáveis ( X_1 ) e ( X_2 ). Aqui estão os passos simplificados para calcular o PCA:

Passo 1: Normalizar os Dados

Dada a matriz de dados ( X = \begin{pmatrix} 2 & 3 \ 4 & 5 \ 6 & 7 \ 8 & 9 \end{pmatrix} ), normalizamos cada coluna.

Passo 2: Calcular a Matriz de Covariância

Após a normalização, calculamos a matriz de covariância dos dados:

[
C = \frac{1}{n-1} X^T X
]

Passo 3: Encontrar Autovalores e Autovetores

Supondo que obtivemos os seguintes autovalores e autovetores:

• Autovalores: ( \lambda_1 = 2.9 ), ( \lambda_2 = 0.1 )
• Autovetores: ( v_1 = \begin{pmatrix} 0.7 \ 0.7 \end{pmatrix} ), ( v_2 = \begin{pmatrix} -0.7 \ 0.7 \end{pmatrix} )

Passo 4: Projeção dos Dados

Finalmente, projetamos os dados nos componentes principais usando os autovetores.

Conclusão

O PCA é uma técnica fundamental na ciência de dados e aprendizado de máquina, permitindo a redução da dimensionalidade sem perder muita informação dos dados. Embora tenha uma base matemática sólida, seu poder prático está na capacidade de simplificar conjuntos de dados complexos e torná-los mais manejáveis.

No próximo artigo, exploraremos casos práticos mais avançados de PCA e como ele pode ser aplicado em diferentes áreas, como processamento de imagens e aprendizado supervisionado.